Bruchgleichungen sind von Schülern häufig gefürchtet. Aber warum? Ganz einfach, weil da immer so ein komischer Strich in der Mitte von zwei Zahlen oder Gleichungen ist. Die meisten Schüler denken auch, dass man dabei unbedingt die Bruchregeln beherrschen muss. Falsch, denn mit den Schritten die ich dir jetzt zeigen werde ist das nicht der Fall. Selbst wenn du jetzt nicht 100% nachvollziehen kannst, warum du jetzt genau das rechnen sollst, ganz egal, du wirst trotzdem zum richtigen Ergebnis gelangen.
Was ist das?
| Bruchgleichungen sind Gleichungen, bei denen die unbekannte Variable mindestens in einem Nenner in der Gleichung vorkommt. |
Beispiele:
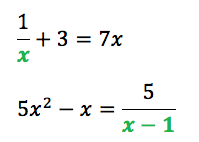
| bedenke:
|
Wie kannst du Bruchgleichungen lösen?
Es gibt zwei Möglichkeiten, um Bruchgleichungen zu lösen:
- grafisch
- rechnerisch
Grafische Lösung
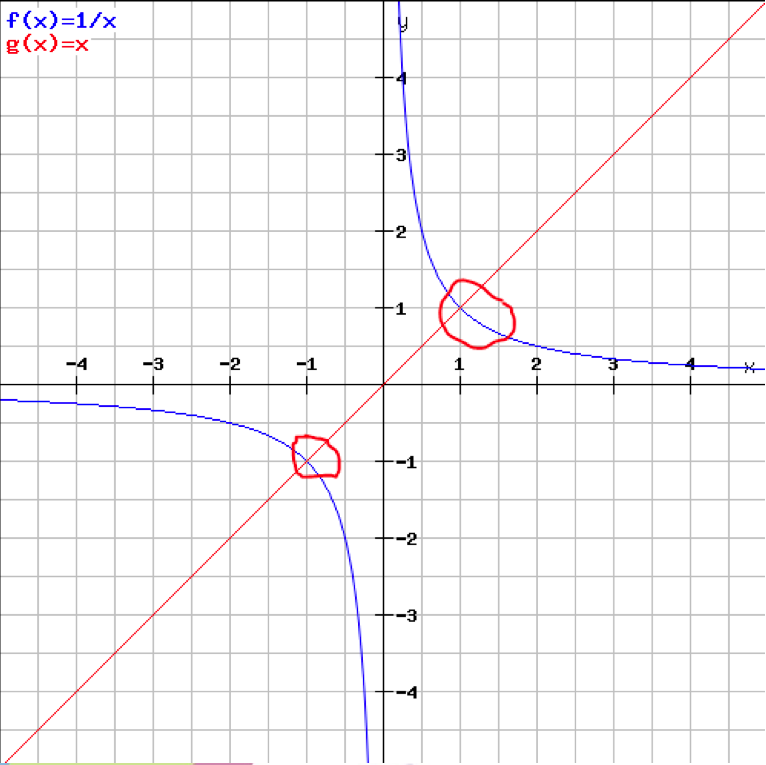
Um solche Gleichungen grafisch zu lösen, musst du nichts weiter machen, als beide Seiten in ein Koordinatensystem zu zeichnen. Du betrachtest also alles, was rechts vom „=“ steht als Funktion und alles was rechts davon steht auch. Du zeichnest also beide Funktionen in ein Koordinatensystem und liest die Schnittpunkte der Funktionen ab. Die Schnittpunkte (x-Werte) sind dann die Lösung(en) der Gleichung. Da das allerdings in der Schule nicht als genauer Lösungsweg angesehen wird, musst du die Gleichung rechnerisch lösen.
Beispiel:
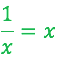
Jetzt betrachtest du und als einzelne Funktionen und zeichnest diese in ein Koordinatensystem. Jetzt musst du nur noch den x-Wert der Schnittpunkte ablesen.
In diesem Fall sind das die Werte x=1 und x=2.
Das sind gleichzeitig auch deine Lösungen der Bruchgleichung.
Rechnerische Lösung
Beim rechnerischen Lösen der Gleichungen funktioniert das nicht ganz so leicht, wie beim grafischen Lösen. Wenn du allerdings weißt, wie es funktioniert, dann ist auch das ein Kinderspiel. Ich zeige dir hier eine Schritt-für-Schritt-Anleitung für das Lösen von Bruchgleichungen. Diese kannst du bei jeder Aufgabe anwenden und kommst immer zum richtigen Ergebnis:
Deine Schritt-für-Schritt-Anleitung:
|
1. Definitionsbereich bestimmen
Der Definitionsbereich gibt an, welche Zahlen du für x (oder eine andere unbekannte Variable) einsetzen darfst. Bei der Bestimmung ist es aber viel leichter, wenn du dich fragst:
„Welche Zahlen darf ich denn nicht einsetzen?“
Im Definitionsbereich sagst du dann, das du alle Zahlen einsetzen darfst, außer zum Beispiel die
Zahl 2.
Du musst dir hierbei immer alle Nenner anschauen, in denen ein x vorkommt. Dann überlegst du dir, welche Zahl du für x einsetzen müsstest, dass der Nenner Null ergibt. Das ist dann genau die Zahl, die nicht im Definitionsbereich liegt, denn der Nenner darf nie 0 ergeben. Warum? Ganz einfach, denn ein Bruchstrich bedeutet das Gleiche wie das Rechenzeichen „Geteilt durch“. Und du weißt ja bereits, dass man nicht durch 0 teilen darf.
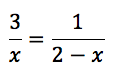
Betrachten wir zuerst einmal die linke Seite. Da ist es ganz einfach. Wenn du für x die Zahl 0 einsetzt, ist der ganze Nenner 0 (klar, der Nenner besteht ja nur aus dem x).
Die rechte Seite ist auch ganz einfach. Welche Zahl musst du für x einsetzen, dass 2 – x = 0?
Richtig: die Zahl 2, denn 2 – 2 = 0.
Jetzt den Definitionsbereich angeben:
![]()
Beachte aber auch hier bitte, dass es mehrere Möglichkeiten gibt, den Definitionsbereich anzugeben.
Übersetzt heißt das:
Der Definitionsberecih (D) sind alle rationalen Zahlen (Q) außer () die Zahlen 0 und 2 ({0;2}).
2. Hauptnenner bestimmen
Auch das ist ganz einfach. Schau dir alle unterschiedlichen Nenner an, die in der Gleichung auftauchen und schreibe sie mit einem „Malzeichen“ hintereinander. Schon hast du den Hauptnenner bestimmt.
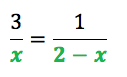
Der Hauptnenner dieser Bruchgleichung lautet also:
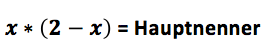
Das würde ich an deiner Stelle noch nicht kürzen. Diese Schreibweise ist meinsten besser für den nächsten Schritt geeignet.
3. Beide Seiten mit dem Hauptnenner multiplizieren
Kein Problem, ab jetzt geht das einfache Rechnen los. Multipliziere einfach den Hauptnenner mit beiden Seiten:
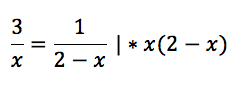
Dieser Schritt ist enorm wichtig, denn er ermöglicht dir, dass du im nächsten Schritt keine Brüche mehr vorliegen hast.
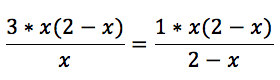
Sieht zwar jetzt kompliziert aus, aber im nächsten Schritt wird’s super einfach.
4. Kürzen
Jetzt musst du nur noch kürzen und schon sind alle Brüche verschwunden:
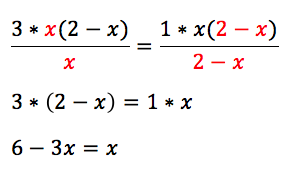
5. Durch einfache Umformung nach der unbekannten Variable auflösen
Jetzt musst du nichts weiter machen, als durch wirklich einfache Äquivalenzumformung nach x aufzulösen:
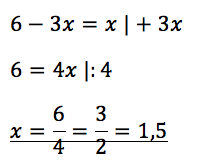
6. Lösung mit Definitionsbereich abgleichen
In diesem Schritt musst du überprüfen, ob deine Lösung auch im Definitionsbereich liegt.
In unserem Beispiel ist die Lösung x=1,5. Im Definitionsbereich liegen alle rationalen Zahlen außer die Zahlen 0 und 2. Also liegt 1,5 im Definitionsbereich.
Sollte deine Lösung nicht im Definitionsbereich liegen, dann gibt es keine Lösung.
7. Lösungsmenge angeben
Hier kann ich dir nicht die perfekte Schreibweise dafür sagen, da jeder Lehrer andere Vorstellungen davon hat, wie man denn die Lösungsmenge angeben soll. Am besten fragst du hier bei Unklarheiten deinen Mathematik-Lehrer, wie er denn die Lösungsmenge angegeben haben möchte.
Ich habe es damals in der Schule immer so gemacht:
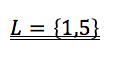
Weiter gehts! Online für die Schule lernen
Lerne online für alle gängigen Schulfächer. Erhalte kostenlos Zugriff auf Erklärungen, Checklisten, Spickzettel und auf unseren Videobereich.
Wähle ein Schulfach aus uns stöbere in unseren Tutorials, eBooks und Checklisten. Egal ob du Vokabeln lernen willst, dir Formeln merken musst oder dich auf ein Referat vorbereitest, die richtigen Tipps findest du hier.