Wie du bereits schon weißt, zeigt uns ein Koordinatensystem immer nur einen bestimmten Ausschnitt des Graphen und die Funktionen verlaufen teilweise bis ins Unendliche weiter. Nun fragst du dich, wie man den Verlauf einer Funktion außerhalb des Koordinatensystems überprüfen kann? Wenn ja, dann solltest du dir auf jeden Fall diesen Blogbeitrag genauer anschauen! Hier wird dir einfach und schnell erklärt wie du diesen Verlauf mathematisch beweisen kannst.
Beispiel:
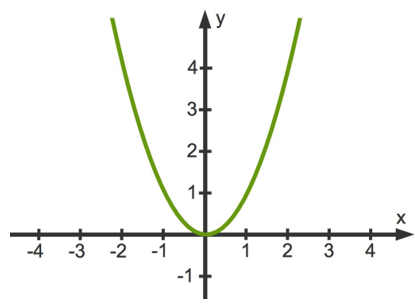
Beginnen wir mit einem Beispiel: f(x)= x²
Jetzt kennen wir unsere Funktion und wissen, dass es eine nach oben geöffnete Parabel ist.
Leider ist es nicht möglich, eine Funktion komplett zu veranschaulichen, denn hierfür würde man ein unendlich großes Koordinatensystem benötigen. Um aber trotzdem sagen zu können, wie unsere Funktion weiterhin verläuft, erstellen wir zuerst eine Wertetabelle:
Nun stellen wir fest:
Wenn x → ∞, dann geht unsere Funktion f(x) → ∞
In Worten: Wenn x gegen Unendlich geht, dann geht unsere Funktion f(x) auch gegen Unendlich.
Zweites Beispiel:
f(x)=x², aber dieses Mal geht x gegen minus Unendlich.
Wir erstellen wieder eine Wertetabelle:
Nun stellen wir fest:
Wenn x → –∞, dann geht unsere Funktion f(x) → ∞
In Worten: Wenn x gegen minus Unendlich geht, dann geht unsere Funktion f(x) gegen Unendlich.
Natürlich musst du nicht immer eine Wertetabelle aufstellen, da dies in der Klassenarbeit zu lange dauern würde. Wenn du nicht auf den ersten Block siehst ob der Graph gegen minus/plus Unendlich geht, dann setze einfach nur ein oder zwei große Zahlen für das x ein.
Weiter gehts! Online für die Schule lernen
Lerne online für alle gängigen Schulfächer. Erhalte kostenlos Zugriff auf Erklärungen, Checklisten, Spickzettel und auf unseren Videobereich.
Wähle ein Schulfach aus uns stöbere in unseren Tutorials, eBooks und Checklisten. Egal ob du Vokabeln lernen willst, dir Formeln merken musst oder dich auf ein Referat vorbereitest, die richtigen Tipps findest du hier.