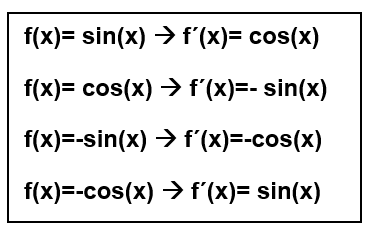Du kennst bereits den Sinus und den Cosinus als Funktion und da du bestimmt auch weißt, dass man jede Funktion ableiten kann, gilt dies natürlich auch für den Sinus und den Cosinus. Vielleicht scheint es zu Beginn erst einmal schwer zu sein, wenn du aber die Ableitungsregeln gut kennst, dann kann nichts mehr schief gehen. In diesem Blogbeitrag werden dir die Ableitungsregeln einfach und verständlich erklärt, sodass bei deiner nächsten Klassenarbeit alles gut laufen wird!
Achtung: Für diesen Blogbeitrag benötigst du alle Ableitungsregeln!
Merke:
Es ist wichtig, dass du diese Ableitungsregeln immer im Kopf behältst. Jetzt wird dir mit Hilfe von Beispielen gezeigt, wie man die Regeln anwendet.
Beispiele:
Beispiel 1:
f(x)= sin(4x² – 3)
→ f´(x)= 8x ⦁ cos(4x² -3)
Wie kommt man nun auf dieses Ergebnis?
Wir wissen, dass der Sinus abgeleitet Cosinus sein muss. Da in der Klammer noch etwas steht, dürfen wir das Nachdifferenzieren auf keinen Fall vergessen. Also leiten wir den Teil in der Klammer noch einmal extra ab und schreiben ihn mit einem Mal-Zeichen (⦁) vor den Cosinus.
Beispiel 2:
f(x)= 2cos(-4x² -5)
→ f´(x)=-8x ⦁ (-2sin(-4x²-5)) = 16x ⦁ sin(-4x²-5)
Wie kommen wir auf dieses Ergebnis?
Wir wissen, dass Cosinus abgeleitet –Sinus sein muss. Genauso wie vorher, müssen wir den Teil, der in der Klammer steht nachdifferenzieren. Am Schluss kannst du alles noch zusammenfassen.
Achtung: Die 2 bleibt laut der Faktorregel stehen, wird also nicht mit abgeleitet.
Weiter gehts! Online für die Schule lernen
Lerne online für alle gängigen Schulfächer. Erhalte kostenlos Zugriff auf Erklärungen, Checklisten, Spickzettel und auf unseren Videobereich.
Wähle ein Schulfach aus uns stöbere in unseren Tutorials, eBooks und Checklisten. Egal ob du Vokabeln lernen willst, dir Formeln merken musst oder dich auf ein Referat vorbereitest, die richtigen Tipps findest du hier.