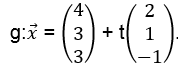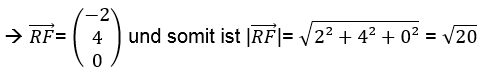Du weißt bereits, wie man den Abstand von einem Punkt zu einer Ebene berechnen kann und ähnlich funktioniert dies auch mit Geraden. Falls du dieses Thema gerade im Unterricht behandelst, dann ist dies die perfekte Möglichkeit dein Wissen zu vertiefen!
Genauso wie beim Abstand von einem Punkt zu einer Ebene versteht man unter dem Abstand eines Punktes R von einer Geraden g die kleinste Entfernung von R zu g.
Allgemeines „Rezept“ zur Berechnung des Abstandes d(R;g):
Beispiel:
Aufgabe:
Berechne den Abstand des Punktes R (2|-3|5) von der Geraden:
Lösung:
1.) Zuerst benötigen wir die Hilfsebene H:
2.) Nun bestimmen wir den Schnittpunkt von H mit g:
3.) Zuletzt bestimmst du den Betrag des Vektors RF:
Weiter gehts! Online für die Schule lernen
Lerne online für alle gängigen Schulfächer. Erhalte kostenlos Zugriff auf Erklärungen, Checklisten, Spickzettel und auf unseren Videobereich.
Wähle ein Schulfach aus uns stöbere in unseren Tutorials, eBooks und Checklisten. Egal ob du Vokabeln lernen willst, dir Formeln merken musst oder dich auf ein Referat vorbereitest, die richtigen Tipps findest du hier.