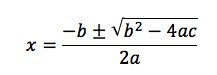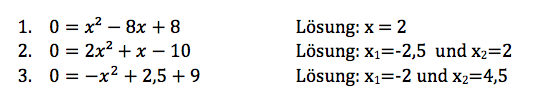„Oh nein!“ Das sagen die meisten Schüler, wenn sie nur den Begriff der Mitternachtsformel hören. Aber es ist so einfach! Auch hier versuchen die meisten Lehrer, diese kompliziert aussehende Formel über zwei DIN A4 Seiten herzuleiten und völlig abstrakte Annäherungen an diese Formel vorzunehmen. Mein damaliger Mathelehrer hat sogar über eine Schulstunde die geschichtliche Herkunft referiert – Schwachsinn. Was du als Schüler wissen musst ist, wie sie lautet und wie man damit rechnet. Deshalb habe ich für dich die wichtigsten Informationen zusammengefasst:
Ich möchte dir nun erklären:
- Wann man denn diese Formel anwendet!
- Wie man damit rechnet!
- Was die Lösungen bedeuten!
Wann wendet man die Mitternachtsformel an?
Diese Frage ist einfach zu beantworten. Ich könnte dir jetzt erklären, wie man denn die komische Formel herleitet und warum man sie genau dann anwenden kann, aber für das Rechnen hilft dir das gar nichts.
Wenn du eine Gleichung der Form 0 = ax² + bx + c vor dir hast, darfst du die Mitternachtsformel anwenden.
Ganz wichtig: Die Gleichung muss immer nullgesetzt sein!
Also zum Beispiel: 0 = 3x² + 2x – 4
Da kannst du die Gleichung mit der Mitternachtsformel lösen (Gleichungen lösen heißt: „Was muss ich für die Variable x einsetzen, dass die Gleichung stimmt?“)
Wie rechnet man mit der Mitternachtsformel?
Vergesse nun mal alles, was dir dein Lehrer darüber gesagt hat. Ich möchte dir jetzt zeigen wie einfach es ist, richtig zu rechnen:
- Entscheide, ob du die Mitternachtsformel anwenden darfst!
- Welche Zahl steht für welche Variable (a, b & c)?
a ist immer die Zahl vor dem x²
b ist immer die Zahl vor dem x
c ist immer die Zahl ohne x
Nicht vergessen: Ein Minuszeichen gehört auch zu der Zahl!
- Setze die Zahlen in die Mitternachtsformel ein!
- Rechne zuerst die Wurzel aus, denn diese entscheidet, wie viele Lösungen es gibt.
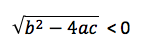
Hör auf zu rechnen! Wenn unter der Wurzel eine negative Zahl herauskommt, gibt es keine Lösung, denn eine negative Wurzel gibt es nicht. Schreib auf Blatt, dass es keine Lösung gibt, also eine leere Lösungsmenge (je nachdem, wie du es laut deinem Lehrer aufschreiben sollst)
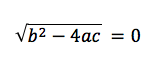
Es gibt genau eine Lösung. Unter der Wurzel kommt Null heraus, was bedeutet, dass du sie einfach weglassen kannst. Die Wurzel aus Null ist nämlich Null.
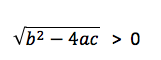
Sobald eine positive Zahl unter der Wurzel herauskommt, musst du die Wurzel einfach berechnen. Das Ergebnis musst du dann schließlich einmal mit dem Wert vor der Wurzel addieren und einmal subtrahieren (Also kommen ja auch zwei Ergebnisse heraus).
Nun hast du also entweder keine Zahl als Lösung, eine oder sogar zwei.
Ich zeig dir das jetzt einfach mal an einem Beispiel:
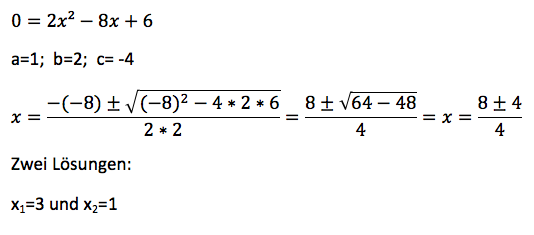
Was bedeuten die Lösungen?
Würdest du die Gleichung y = ax² + bx + c in ein Koordinatensystem zeichnen, würdest du immer (ganz egal welche Werte du für a, b und c einsetzt) eine Parabel sehen.
Setzt man diese Gleichung Null heißt das doch, dass du damit die Nullstellen berechnest, also die Werte, an denen die Funktion die x-Achse schneidet.
Bekommst du beim Rechnen mit der Mitternachtsformel also kein Ergebnis heraus, heißt das, dass die Funktion auch keinen Schnittpunkt mit der x-Achse besitzt. Das ist beispielsweise der Fall, wenn die Parabel nach oben geöffnet ist und sie ihren Scheitelpunkt über der x-Achse hat.
Erhältst du genau ein Ergebnis, liegt der Scheitelpunkt direkt auf der x-Achse. Berechnest du den Wert x=-3 heißt das also, dass die Parabel die x-Achse beim Wert 3 berührt.
Bekommst du beim Rechnen zwei Ergebnisse, sind diese Werte exakt die Punkte auf der x-Achse, in denen die Parabel diese schneidet.
Aufgaben:
Weiter gehts! Online für die Schule lernen
Lerne online für alle gängigen Schulfächer. Erhalte kostenlos Zugriff auf Erklärungen, Checklisten, Spickzettel und auf unseren Videobereich.
Wähle ein Schulfach aus uns stöbere in unseren Tutorials, eBooks und Checklisten. Egal ob du Vokabeln lernen willst, dir Formeln merken musst oder dich auf ein Referat vorbereitest, die richtigen Tipps findest du hier.